Dangers of recursion (python vs rust): Fibonacci case
Fibonacci sequence is commonly used to show recursion, but may not be the best algorithm to compare languages and performance, since the recursive implementation is not the optimal one and languages like python will outperform rust or C.

I'm learning rust and while reading a post about it being "the new big thing in data science", at one point they compared a piece of code to its equivalent in python. An alarm raised in my brain: I implemented it two days ago in rust and it took way less than what they were reporting.
They used the Fibonacci sequence using recursion, and it seemed fair: it took 0.3 s with rust while python took more than 22s If you got maths a bit rusty, Fibonacci sequence is defined as:
\(F_0 = 0, F_1 = 1\)
and
\(F_n = F_{n-1} + F_{n-2}\)
for \(n > 1\)
The typical way to reason about it is as a recursive function, so the first thought is to implement it like so. But WAIT! I remember computing the 94th number of the sequence in an instant with the function I implemented in rust a couple days ago. If we were to follow the same timings, and assuming we have an exponential cost, it should take several minutes!
I quickly reviewed my code and there it was: I did not used recursion. My implementation was just a couple of mutable variables and a sum. Every Fibonacci number was calculated only once, instead of an exponential number of times.
fn fibonacci(number: u32) -> u128 {
let mut minus_one = 1;
let mut minus_two = 0;
let mut current = 0;
if number == 0 {
return 0;
} else if number == 1 {
return 1;
}
for _ in 2..=number {
current = minus_two + minus_one;
minus_two = minus_one;
minus_one = current;
}
current
}
I promptly timed it, and there it was: the 40th number of the sequence was taking 40 ns (nano) That is waay less than they reported (just with cargo build --release). I then implemented it the recursive way, in two different versions just to see how they compared with eachother.
fn fibonacci_rec(number: u32) -> u128 {
if number < 2 {
number as u128
} else {
fibonacci_rec(number-1) + fibonacci_rec(number-2)
}
}
fn fibonacci_rec_v2(number: u32) -> u128 {
match number {
1 | 0 => number as u128,
_ => fibonacci_rec_v2(number - 1) + fibonacci_rec_v2(number - 2),
}
}
Both of them took 217 ms (milli), several orders of magniture higher and much closer to what it was reported.
So we know the way you build the algorithm matter. Let's go to python since I was assuming it will probably happen the same.
import timeit
def fibonacci(n: int) -> int:
minus_one = 1
minus_two = 0
current = 0
if n < 2:
return n
for _ in range(2, n+1):
current = minus_one + minus_two
minus_two = minus_one
minus_one = current
return current
timeit.timeit("fibonacci(40)", number=1, globals=globals())There it was, python(3.10) had a much better time than Rust recursive with ~5 (micro). We can see that the way you build the algorithm matters more than the language itself, at least for this simple calculation. I mean, it does not take much experience to know that, but I wanted to write this post just as a reminder since it looks like Fibonacci sequence is always used to explain recursion when you learn a new language.µs
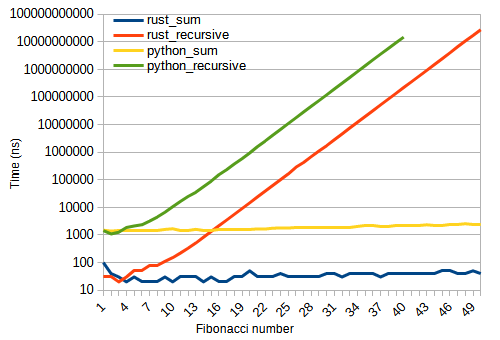
log format, so the time it took to compute recurivelly the 50th number was 27s. We can see that while python takes loner, there is one point where algorithm matters more than the language. Not scientific and it's just for illustration purposesNote: probably Fibonacci sequence is already used and studied in benchmarks and what I'm writing here is not new. But can't you let a simple programmer discover things by himself? That said, if you have any interesting link let me know at my Twitter feed!